Playing with Probability - Efrons Dice/Activity

This lesson idea is also available to download File:Efron's Dice Activity.doc

Efron’s Dice Lesson Ideas

Pedagogical rationale: We are used to the idea of transitivity, where we can ascribe an order to events. Efron’s dice are non-transitive and probability methods that the pupils are familiar with can be used to explore how to play a game using them.

Learning Objectives: To see the worth of probability tables and know how to use them to solve a problem.

Introduction: I have some large wooden dice that are coloured green, yellow, red and purple. I have added stickers so they have the numbers shown on the nets.

I play a game against the pupils where they choose a die, I then choose one and we roll at the same time, with the higher score winning. Pupils note that it is impossible to get a draw.

If we play 10 or so games it is very likely that I will win if I choose correctly. The pupils then usually want to choose the die I had used, so I pick a different one and can win in the long run. The same thing happens again with a different choice.

Exploring the problem in pairs

They then need to explore why I am winning. The pupils are invited to choose two dice and to see which one wins. They can use any method they wish.

One common method that the pupils use is to compare the numbers on the dice. For example, if yellow is compared with green, yellow wins if green rolls 0 and loses if green rolls 4; the probability that yellow wins is 1/3 and the probability that green wins is 2/3.

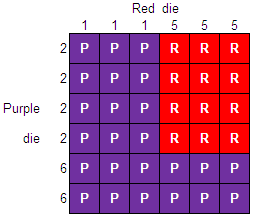
When it comes to comparing red and purple this method is more difficult (but still possible). A better method here might be to draw a probability table:

The coloured letter shows which one wins; the probability of purple beating red is 24/36, which is 2/3.

Rather wonderfully, the probability each time is always 2/3, with the colours having the advantage over each other in a circle.

p(Purple beats Red) = 2/3

p(Red beats Green) = 2/3

p(Green beats Yellow) = 2/3

p(Yellow beats Purple) = 2/3

It is not obvious and is rather surprising that this cycle exists. I usually put the purple dice down, with yellow on top to show it is better, with green on top of yellow and red on top of green. Then I take purple from the bottom of the pile and put it on the top.

Extension

The pupils are often intrigued as to what happens if they compare purple and green or red and yellow. They are welcome to do this.

Pupils can be asked to try to find a set of three dice that has this property. This is possible, but difficult.

Drawbacks

Any practical probability starting point carries the risk that the results will not, in the short term, produce the expected results. This is a useful discussion point.