Number and representation game: Difference between revisions
JanetBlair (talk | contribs) m (added guidance notes) |
JanetBlair (talk | contribs) m (edited ten to 10) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Maths]][[Category:Primary]][[Category:ORBIT]] | |||
{{Rinfo | |||
|type= Lesson idea | |||
|attribution= John Golden | |||
|title= Number and representation game. | |||
|tagline= Interactive GeoGebra investigation that allows children (age 6-10) to explore an element of mathematics for themselves. | |||
|image= Number and representation game.png | |||
|topic= Visualisation | |||
|subject= Maths | |||
|resourcenumber= M00XX | |||
|age= Age group 6-10, Primary | |||
|content= Geogebra has been used to create a simple interactive applet. The applet and guidance notes on how to use it with students are included with the resource. | |||
|related resources= This activity is a result of the 2013 [[ORBIT/GeoGebra Competition]] that asked entrants to create an open-ended activity that supports interactive teaching and active learning for the 6-10 age range. | |||
|other= | |||
|final=yes | |||
|licence= | |||
|format= Embedded GeoGebra applet and guidance notes. | |||
|resources= | |||
* GeoGebra file: | |||
[[file:number and representation game.ggb]] | |||
* Guidance notes: | |||
[[file:number and representation game.doc]] | |||
}} | |||
<ggb_applet width="669" height="541" version="4.2" ggbBase64="UEsDBBQACAAIABiCPEIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ6VWCTRb6xZOCVJDUa3eIuS2VVcUFy23V4mYVZs2VFHE1EtNoYh5KjXVpfQaOpiCNlpNQg0pCToppaYaIubhxlANglBD4p3et9Zd66377nvrrbf+ffY+5/zn7H//5+z97S/1MspMTFhGGAQCiVmYG1sBtg04yiGCgH78HP8OBBLxsjBGXgkbZhXY+x6ylU4KTziqrL7CBwELm6e6wLTegiWOVhkfcMuKB+3XOBXjcmZy6KR2Jkj7O7nK1y7Gca6Hd2RkE25JQFyFElV9X/u6SlYM2SarTv3KU8FV3BzOoJ57KbsW/QmdV7FMhNtMkLE2Y9ZMYUGQidUtJ1AcDATh+6YOPojicughzPbDOgWFhVhx+XOVnt2FjOmWNNbOcjOlq0A3ueacOg5zxDL3VBUyQZDR/9SaWFwcpyCLNDRLD5/9+CBk6o1AxWV8vN/oy946vxEPoyTRqtFRR59PZalSszzuDrmfGr0T0sM8bDM39TY5ZK4LujehjqFVph1RH16b63Z+Sm5WXPhN6dKX8cZI7HjnI500Rwp5l9zM876rgAhZi+LUYce8lVD5le/TZan8+2ApBPkyHzqp7kbvscjNsVBVRcUW0ww5r4nozQKfL7U+9DrTdBn7x+dzvuQ5x1QFzXXZ9z25SLTMUxssMRGJLRU9VBYA3X8ECmXNenp4DDOqPYkRnM+DFH/njg8ftoy4DbjFa9xtDtGt5Q4Jw2zP8ZvvwSPpxNVa74EXwIOMVWYHMXxtdhBvJCSrg813KPy9d/OepMSJ6xlQXY+BZzbVMdxtxvpCnyoc3n5Gv+BeOXvgqXUrlDswOQBSvNt+J1fV4ecqYZ2VN7j+R77DNR8aQpeXcvdm7iKGdZdp7lJKqGA9k6ltMZnTAYt5lztyVauBxRhKRVEHg8f08f0+UVvMPGxTe+PmeCTJ0df3uYMgLEUJ0xTlZfPsys10K4KB90uF2F22CsGySfBpknbIF7vFgYq8R4RSzjObivhCN4HB3l5H3JMLD6adNz78pkS0r/YYLDW7i+jfzPEaqsSzxhtHOJoHTww18NN1YnbDfPqepEP1IvpT1YO353WZfGC2MQFVMOqVG7bH3VQ9c6a27X3M1uovdLsRir8/VDdEdJj/EKm00IJvY3li4tlVoreWx8fKSwhuf4G0ql1l8bt4sEPo5DbJuRnrN1KH4zjUejNnB57b9zk574vPVk5UJ1le4y30EXjNRk6mFnSiSIiBBAi8XydPzemFUfIBRtZxs2PwmotbW1u7BpCDmA3WyBwq7ZhGsM4FnaMg5Bt4CpaRa5KvHz0sppZbswvkE2tzInbOzDBzpcqzW56KW8xVVFKiOjx5KH/GO3tntxpS25UieXwUSrh3yqHKvfXADosy8TVL4kRUuSTc1vI4Qyah57uEJ7YkxwXBbWk1xxtvk8VDKW5nhMlZ4Rzw6883QJeODztHsRNl+3q+mhfpR49GXfSJMTVNkhUVdWxq92b8dvJi4OKn2uTc5l86pMHIzJXVt+KIoa21OVUNjV6n71Q4Rn3eX737vWvYbDYp2fz8+UAxO2bCQGpaWrWWZ9dQ3D5+RxKdPdOqevLk+5wBgn/h9U/lVP+th+RbCI6HjN25gMm4ilKaBjN4X/ztdKByqGh/i+Ju4L9S5Z4BmU21LgfWGsk/G+RYSkdj0q8x4wfQyzB0NlYzbMVFN2yl+BFZc7ufVlNzmvL8FXOn3fsao57BYJBQGEzhXNUh8K09kcVBosrGVZ9yimfs9gLBrVlkV39olX9uoQYVjomDuRp1X/ky0Yw4ZvThTlNWuEFmZfEugbNIp1oTzYX9pPgT/wkygPLXiZg8f6QbIyVhQ1lZm4uDMQXF4HCdZ6fxu3CDzMDUg7KcSqtyfJ7GvIDow6vqfBArNfTM4NrEed1ed2qEawKPV90DoWGVfB7Kg5HtqhH6MwAcaPsO/ZgnXYK++Tjxh5YyBwoWlV9hS26IUm10Ufv++9cWZc0DaeVLAIYxsiBW+mhNfKHBlaYcqyvZYeU0eKfsTwHFUoYWSe0EK/kczGyxKGb/YyQipw8nCjOvv04nOS2Z3DyITNdXUek4eeH+ZOHaDTqpAKFFwS0OqmWh9dI0o3MEnmeHDQzsVIOQ7YpACYSSt0/JfbZYH032/zmg6dMQfwc8ESxR5liyKOxsip3q4VigJwRMp2yzmlDrs6aNVBU5dKmpGDh8pMel6EUs58VP6vgGYFM/VLNsjMSOTDnqxN+WfFy0mJ6MKT2lgDcBagEpYSAB3vd35r/NfzP/YT7T1uJj14vsWi29FkTz56V67G67RSHlrHLknTlOAwu1OFWPNVSu03VcCdm0+tGtUzTya9kr691IQ4VuXPIcapPWqRyupUem1IwU0Daagy38IZB4WBwMwvcXwzSWeI+UACPv3MoKBn87+YuErwl4rduI011o75zdEauOmwkae2xa554MvW8twpI6FqswIoac/2P8u9f/N3kDNx8qFLLg8M61Jc+UWG6ea/N8HCZ/XbQ7oeePAQNC/hvJVqaNQQEfgBfQXwxy/CryfM4Sz97r01gjIT22rRkBSf0Z9/m2n5yx+4/rsHWYpNjxhb93/t8lC94m5N4QgeLyOoo9xvvGWrNnWUtTF0KXM2Drf4z/xzlkdVsg1V6z68xVdTal1+kcneu7Zdw9kp+t17IWcXjPfBHIkNE7H3VQEuNLB0B/VvpKUsDCJ0Xd4PlM6NnAsnf4VQCuIQfhoUujVUQHShLtraWs/xtx6adyPwW8KkTEygcCAKKANDTRZbWkHXFNNd97fSwnQUh8GGhLhhnROxvfm5fP38BcviyRm7KucMqqN8a6u+jeveljQIE3cTccOjo6qgE6UL8c3wIAvuS7NFjo8jguKyfnFzQanZuV5Rq58YXdLS5dapr+or//ikOdr30V806aEzWkd1ivOElNMkn06DTKmuxY76YXuVEDYKFu5Mbz6LVOHe3A380dmmMaiddq2zW1tPx6S0zqguZQYPaxNgDiuJJSUu62ZAxO1143hD3dgm29K6837ObuzmUmHYB+DuH1lppxJ8iYxuHpmZmC0w/zAHYF7AZndvaikJp1R0+t+O2upTEq602iyMbWXNEIwI1Yo/VBWITl/aJYHqOktJS1u7VGurA83ui3+5WtHb76e8rEhKRKG/CVuHgosUD2pbviW6Br+U6+usUL3L55Ir4rmdMYcx+gQMM1Xn2+Q5Wu2PFUKSXfV3H7SDR9/ryn4Y+0/UpqI11aM6Ahn/uV04A2U1Z2gkIOCgoa8y95pFDt0RnYBzCl2rNBs3aBgS86ixAT2v7jv8IwYODOrwiA/zBDeECQY179QNjfmhj06fbm8rI6odAw1Po0aweDuB8hjNtMXJzXCnjwkGANghQAjb6e/+pNfLRzWASA2ZBpk8yZ1rtC6dNNKvDg9sc/fNDE9Sf0oC8VJ1iXV3l0yoD3Hx7ztqHIZdhVuQkQx/gJl4rq8vPlQuOUvcppWBrMPGV+o0jt4YAdTtLpKp6zMHjCwFiE708++039ywWEbyWJjTjuzss8qoYJArg3yMIEZUwydIn/B1BLBwj7JnAkawoAAKILAABQSwMEFAAIAAgAGII8QgAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAAIABiCPEIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V35ctvGGf/beYotM+NJpxKEXVykLcXjuE2bjuJ4ZLfpMZ0MCCxBhCRAYUEdmTxA+xT9q9M+V56k3+4CEHjgIgFZMpTWAhbY6/vt7zv2IHn66mYxR1c0Yn4YnA2wog4QDZzQ9QPvbLCKJ8fDwasvPzv1aOjRcWSjSRgt7PhsoCtkcFcOUgrWeGHfPRtMbHeoa6Ph8dAko2OdTNxjezSxj3XVmUywZWnGZDRA6Ib5L4Lwrb2gbGk79L0zpQv7PHTsWNQ5jePli5OT6+trJW1dCSPvxPPGyg1zBwh6HrCzQXLzAqpbK3StiexEVfHJX749l9Uf+wGL7cChA8SlWvlffvbs9NoP3PAaXftuPD0bmCZ0bkp9bwpimiNtgE54piXIuqRO7F9RBkVzSSFzvFgORDY74O+fyTs0z8QZINe/8l0anQ1UhYyGI0MzTYKHRDOxZQxQGPk0iJPMOGn0JK3u9Mqn17Jefiea1NWRBWPgM388pxz1OQOx/GASAaTQo2gFSRbfzunYjtL0XYfwEfwPMvg/UV4XjJ3E4WxAVPMIG8aRpapHhqHKvuQbHqA4DOeiVhUZI/Tzz4ioREVH/ILlhcDFNOUrVT5TNXkh8qLLiyHz6LK4LrPqMo8u8+haiZxJ+k7Q5MGapKmcWl5ODPLxfyb8EwBsyDnMyYm5ED8jzHsvLhri/cai//yiJ0lTJi1xwaq84OTlkP8ReJkHSqTtJRHOtSr5UNzoFl/SFk1jWL9FcpCcmZRkl5TEKJDyQHDTRrGRaxTaEv8X/7aa1BrJWQhtgxZN/RDd36NBS11T+1Tn5RUn1zIYWuvU6UlqDU+TDiE25XkTSsd0wXgXtZEwTggjA5TXtMCWGAiP4GJxJSYIG0g3IImHyORXC2lcb3WkoSHi+bCGhAkyhvBHFzptIgPq4g8tqdxI05GhISwMl44ABSSMH2BCNMhhGMiAQrx1zJvVTKSbkNCGSIcOcrNncdOiQTlIQ+MEaRhpvCy2EDGRSZDFTSfWuUU1h7zvUClBpopMXhRsJ9hNaTOhxBBpXBrQgmXI/AzcKZ0vs1EROPrBchWvYecs3PQ2Djdyu6Ez+2oDa2qzOL2HTOCw7vyidGBrbvPZ6dwe0zkEF+85DRC6sudcy0X9kzCIUUqBoXzmRfZy6jvsPY1jKMXQj/aVfW7H9OZryM3SDoqmhTc/pStn7ru+HfwZOMKr4BWizLlz25U6d8MwZStOGEbu+1sGxEE3f6NRCO8sRc39h4HYt/KNbhJllP8PFJE5Nme8oa4VUuHNbcErrMum6VUmmn1DM4GQF8lIKkt8w74K53ePlqEfxG/sZbyKRKgGljLiUr0OvDkV4Ioxh6DHmY3Dm/cSVU3W9eF2CSlV9mDsvQnnYYRAI4kBgYiXXMfyKvLwrmW5VJFHFTnUdJh8N3uPR0TkENexvIpcMO6ya4moOBUTq2kzPhO2BiqXLEuNM2cNj6FWgR+fp4nYd2Z3ovICb1eLMRAuYeR6nbitOk9PNjh2OqNRQOeSSQEM5ipcMUntjJ7PTleMvrPj6evAvaAe6OQ7m5vFGKqWWe+67FLHX0BB+TwBz+YD+yfoqnzqUi+iqYhzER1LaMVbNc/rrceiqq+jcPFNcPUBWLPR1dOTVJ5T5kT+krMTjcFOz+gd/1yf2WDl3Xw5EJ6BFA63OABkzEH8Nowgt72Kp2EkgmDQXZBpiP5oBys7ugVzCawUUXgYzdiU0vgDvYmRPQ6vIOOHKUUewPQCrPVybt9ytIBlMbUXTHn+OVZffgdRNk8ij8YMxVOeCpBwOcgOXPEkhD/RRi7Xd6iC3kWUyfRbcHPJUIPp4/mQzYFZQa7vwQRNZfmpzdACZEJuGLNX6MPUjuUL5sBTUGKpmQr62o9Y8gqqs+Rjxt1a0nHx5/0KDCRoqT2f08ADMcVTLHPzyZbo22Strojac27Trqdh1h0FfaEif8Jz3yJvxYWShcZg4G3o7nUUBp7ya/TBh05y4dSkR8rOFmVbXLisBZHvHYwB7wN4sqQ4qDidc7UCMlEW+57w5i9E7m84tD4HZWL7kRjIVwA5jCy6DVeipRAocO3HU04MOwcM5w36PQ1/L2ad0A+YdU6n4WIMPQEuemwZxooTLhLiLRZ8rAMRZ7wL57deGAzuPJytng2+UI+Q+mugIpb3mN8TuMfJvSbvIY9QknAVp0WXUCGWJW1ZaCzzO3DRQRel1iS94D5oThcwmUOxsLPLpD+pxZHVrRtEgMmZwVSPydlVYp/FzR9816XCg4t+cZOEwvGP4FOzEErWm7M18H7DXGNVGmODCzJfTm0+DVUT8y4Ua81EiCq/Dd284QC7J+XakpBRj6eyntiD1nvapKOJ4WPo5mxwLJY0bmUd6Kd8XXuAD6SY34I5/CbgdpsKS7dt6WeULrmL/S74ENkB40sm6ya+PpLjh4OkmgCJEyAFso8HSefhILlJyUeGpPtwkEw5eYwfqHave6YLuAWXte6YEs9ibrmdCy2g1+WuJVgtaOQ7GfSyiFgv5JGL7JeRYrI9GmkQfzcUuFUJSHMJyA4J8MeTADeXAH9ECYi6JcJ5YwnOdwlgHiTBeoNXoFthlLW32jYo63O0Uouy3XpDc2IHMNsScxYW06Wc9y0plVPGzF7w2YeYaec6U2zSy+0QKbdDuWkbk1NRx45iymDC2QjX4PHjuhl03Beu6xonDP0cZq4bSpebGAS7Zw3P7WXIXu4xP0gKPu5ZQgMUE3mrsTwQ0X7i2hDdVjDuM9LVeJPm6JL+YCmRW5Ux9Qe8Nz9/eOyrL3va1VI8D0a1r9g2RLglnPuNdjXmWnN8td5gScqQI/t6f9JPj/9DqbfSm+Oot4Ngg6neR4NQL4VuXyLqPSOiXm0O9cMCe72XIb1eHcbrhzr1zQp6hu26Cd2NsdEcVaM3OBqlyO2r70bPNN2o1nTjMAtq9NmCNrSjrXipPiNdjbfZHF2zN1iapcjty06zZ4w0a7DwMH03P1lNLzjCNswdYYN7kh1hU5OEliQKDrFZsiyVxSaygCcPsU2b428VY250gvmBW5L1j7jQQ464HLxxmju9Rjb2le+24feB/d6PCk0eCI7pNjJJT1zpjwpG74HAuMnGY1K+H//QcJw+EByzY2uk1rGGjw3j5rGST+hcCVGMB3quJPHVwe7Iydo3ZrKqoqUH77nXIXzjR858E78vVMWAIEgxkmBJVXRjC8ZZOXhOGOSOxM3qWw4o6PqSnpD9uyT3OfrlX/9BeBuf9DNX2wjppJle7ENd6ns0kPrNELpR05Nsamrk0yc3AOOx1BqcHsfCuXONoJGRf4Nep/lfp7lekzPxgXf+GffXWlLta13Uxh8ZyZ3szmWwpkf8o4P+BMZhLzWaFc09ZnW0Z4MAOb05mAaknzQgFTTAHdGgfCI6qz8J3UmJNomh9ZMYJieGnvtIbTFHSKccacCUA/nSJmv0frIGV9kT7R64UrHI1YQfy3bYYPSTDaQqyNC7YcOycNu9uYVYtmkV0g/V944Iu80C7poIhWZhmxqXTUhx2Q4dRv1kA9Yr2HAfTqKIBzsoU3WGpDKkSM6QHMyXYT/5MqygS7fxZy2iHECRtshh9ZMcetU8BXc+l61gyF7caIsVZj9ZURVvdLW6VXX8OGpChWjPNf0+DHDl8gTpeqyjwjFuPsmIWp1k7FjRzq/4C3p8gpQoWHvQuiZCfgunxv7QgbtEn9heUaF2lQdf0b4LftEWiofr2w4f2wd9K1jd0Ts3vOXre9H+cflm0XbosWNnqQ/0KJjla12H45uDWEAT1oQYrCUq7NhL6gUVds/gta5n8Kxw8Js7Dtaqy9ixPdQHIpAqm9DRyh8rdxls32iCdRBN7Ngr6gM1tKrovaMtgvWAsE5McWDQ2SpZdiz69YEsBftJ+r3GFuWUiZsQJG6JDjs2CHpBB7OCDh3FF3Hh4De3EXGrdmHHzmIfiFDgRPSu44u4whbs6zji9l1G9m2UPaOGXrVacWB8sfvQ81DR+KFnLTv0TLYPPTvNFimcwxcmLjBQ4d+IoF/++T+UJPR8wswnKgLSu0XBbCAeP1vMoTLClpH9NAjZ5A0MbLbKpXXEG6xYZbxxm/HGbY032hNvinhjwZjV5A3k7Io3ZayhzVhDW2NNxSr5J0kHc6QMSY4OuIwOavt0GFWQYdKMDJPWyIDzhkLru9UYYmWkbccmI3HXHTkUqzI28ZoRxHvyMd2zZaQrGOfPPmzzxuoyNhG8KTUr02asmT75mEPoYCgqqUeH7sxIRag6a3gG7mmKcw+8MfkUpyZvDgpVi1ZNnGx3dseBmWaMWbbAGJJnDMkzhuQZQ3rLGMtUTLPe5IYowy4YQ0sYc9mMMZetMaaPTgciVtWqN7HpaMnVLaFC1PDYT2tU0J6MRyFjTEWvaTx0hXTBmEkJY1gzxrDWGIPzvND6TpKRpuBh2US4I2PilVAjbkaN+MmY3MOBMhUrQ7Ne8NpRKDItoYzzQ8VPyWzu6JCnUOQALpgKsepxoasPlpZwwW3GBbc1LjxNZIopgzGfydSiTEfByLKEMrQZZWgLlNHylNHylNHylNF6Sxm5WlIrfDUOW3QtYsxlCWMmzRgzaY0x/XQ4eu1dveyrYetyYX3Ytn4FdvMnYLPPYZV8SjT9Msl6n+vCNYcpybfvFz/ucfayhP9eM/57rfFfe7KYxU5Wq30Wwmy6wFyuJhe4x3rCSvRk2kxPpq3pCc5rg/akGmbFhn/LfuOCfJIKUSG09kkKXfNEcokVmDWzArMnb3kfX15Aap/q6GiCwZehirdjG1Fm+TTBOIQLmrp+pMMq5kJjR1F3d62YC5fNuHD5tDxxH5SRB9bLiHJQiD1exXHuC0lksmqno5kvLR+M7yYTRmPxixeWLn4nQNfKxmr/XySwVzf+3Lej2/XfYnh26nlj5kT+MkbyzZ+WLmjOmzBgkEf8xMPf//H8c6y+fE/jP/Oo4+/nR+cBvd54eIGPLvCOx+Togux4rB1daNljjvVZXl/spZBR9OctvUZvV4sxjdjWYN4sI2Arz5pGRwMED8VBqd/wtWD4A7Oxk+qoqjCoqh0vlXcspjcxTjr3/HIVxi+/n4ZoajO0CCP6Sj4abHeUlxusV1Lb7LT+hTfPTich9IwBdJMswmT+T/RbrrS6vD8bDAepFqYB4piF81VM3zsRpcF56EgKC9rrpqC9ZuyhqVUmuBtNxcSQmjokH1lVM3UCsq3m8VFMg0kEHjCnVXeF15TqAw3Q1zzrHqhrHwV1jrZA3Ro+MNRd36mB+G8h1x5g6x8FbA1jAfbwoWFNL1f2fANskdqB+O943nqWmaxZ5r9S9qv6BvngOFCKJoI8XhCCvv+K99mT7fHFxCr8cOu9WHQW21H8LvShLOeLoahG7lsLRzKUgSjeyj+15A/LyR5WD4q2NihvptSZITHWtmf7QYMRqjJYTUZI5K0zRGry240fyeVuDJCuDLX8UBjJAOG1ATILB2jdUIXhnNp3lkrCsxlB3cHS2rpUI+Tq95/3b7P3OU48gO5v6Qf3OWmoi5578Ut0vivM3ZRUFHtckqYxTSLtuZT2oo60WdHHJbHwcZm43MLUklYWe8BKeOLk5pQ87dHQo+PI/vL/UEsHCNMmmJpxEAAAHKwAAFBLAQIUABQACAAIABiCPEL7JnAkawoAAKILAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAIAAgAGII8QkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAArwoAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAYgjxC0yaYmnEQAAAcrAAADAAAAAAAAAAAAAAAAAANCwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAALgbAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="false" showMenuBar="false" showToolBar="false" showToolBarHelp="true" /> | <ggb_applet width="669" height="541" version="4.2" ggbBase64="UEsDBBQACAAIABiCPEIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ6VWCTRb6xZOCVJDUa3eIuS2VVcUFy23V4mYVZs2VFHE1EtNoYh5KjXVpfQaOpiCNlpNQg0pCToppaYaIubhxlANglBD4p3et9Zd66377nvrrbf+ffY+5/zn7H//5+z97S/1MspMTFhGGAQCiVmYG1sBtg04yiGCgH78HP8OBBLxsjBGXgkbZhXY+x6ylU4KTziqrL7CBwELm6e6wLTegiWOVhkfcMuKB+3XOBXjcmZy6KR2Jkj7O7nK1y7Gca6Hd2RkE25JQFyFElV9X/u6SlYM2SarTv3KU8FV3BzOoJ57KbsW/QmdV7FMhNtMkLE2Y9ZMYUGQidUtJ1AcDATh+6YOPojicughzPbDOgWFhVhx+XOVnt2FjOmWNNbOcjOlq0A3ueacOg5zxDL3VBUyQZDR/9SaWFwcpyCLNDRLD5/9+CBk6o1AxWV8vN/oy946vxEPoyTRqtFRR59PZalSszzuDrmfGr0T0sM8bDM39TY5ZK4LujehjqFVph1RH16b63Z+Sm5WXPhN6dKX8cZI7HjnI500Rwp5l9zM876rgAhZi+LUYce8lVD5le/TZan8+2ApBPkyHzqp7kbvscjNsVBVRcUW0ww5r4nozQKfL7U+9DrTdBn7x+dzvuQ5x1QFzXXZ9z25SLTMUxssMRGJLRU9VBYA3X8ECmXNenp4DDOqPYkRnM+DFH/njg8ftoy4DbjFa9xtDtGt5Q4Jw2zP8ZvvwSPpxNVa74EXwIOMVWYHMXxtdhBvJCSrg813KPy9d/OepMSJ6xlQXY+BZzbVMdxtxvpCnyoc3n5Gv+BeOXvgqXUrlDswOQBSvNt+J1fV4ecqYZ2VN7j+R77DNR8aQpeXcvdm7iKGdZdp7lJKqGA9k6ltMZnTAYt5lztyVauBxRhKRVEHg8f08f0+UVvMPGxTe+PmeCTJ0df3uYMgLEUJ0xTlZfPsys10K4KB90uF2F22CsGySfBpknbIF7vFgYq8R4RSzjObivhCN4HB3l5H3JMLD6adNz78pkS0r/YYLDW7i+jfzPEaqsSzxhtHOJoHTww18NN1YnbDfPqepEP1IvpT1YO353WZfGC2MQFVMOqVG7bH3VQ9c6a27X3M1uovdLsRir8/VDdEdJj/EKm00IJvY3li4tlVoreWx8fKSwhuf4G0ql1l8bt4sEPo5DbJuRnrN1KH4zjUejNnB57b9zk574vPVk5UJ1le4y30EXjNRk6mFnSiSIiBBAi8XydPzemFUfIBRtZxs2PwmotbW1u7BpCDmA3WyBwq7ZhGsM4FnaMg5Bt4CpaRa5KvHz0sppZbswvkE2tzInbOzDBzpcqzW56KW8xVVFKiOjx5KH/GO3tntxpS25UieXwUSrh3yqHKvfXADosy8TVL4kRUuSTc1vI4Qyah57uEJ7YkxwXBbWk1xxtvk8VDKW5nhMlZ4Rzw6883QJeODztHsRNl+3q+mhfpR49GXfSJMTVNkhUVdWxq92b8dvJi4OKn2uTc5l86pMHIzJXVt+KIoa21OVUNjV6n71Q4Rn3eX737vWvYbDYp2fz8+UAxO2bCQGpaWrWWZ9dQ3D5+RxKdPdOqevLk+5wBgn/h9U/lVP+th+RbCI6HjN25gMm4ilKaBjN4X/ztdKByqGh/i+Ju4L9S5Z4BmU21LgfWGsk/G+RYSkdj0q8x4wfQyzB0NlYzbMVFN2yl+BFZc7ufVlNzmvL8FXOn3fsao57BYJBQGEzhXNUh8K09kcVBosrGVZ9yimfs9gLBrVlkV39olX9uoQYVjomDuRp1X/ky0Yw4ZvThTlNWuEFmZfEugbNIp1oTzYX9pPgT/wkygPLXiZg8f6QbIyVhQ1lZm4uDMQXF4HCdZ6fxu3CDzMDUg7KcSqtyfJ7GvIDow6vqfBArNfTM4NrEed1ed2qEawKPV90DoWGVfB7Kg5HtqhH6MwAcaPsO/ZgnXYK++Tjxh5YyBwoWlV9hS26IUm10Ufv++9cWZc0DaeVLAIYxsiBW+mhNfKHBlaYcqyvZYeU0eKfsTwHFUoYWSe0EK/kczGyxKGb/YyQipw8nCjOvv04nOS2Z3DyITNdXUek4eeH+ZOHaDTqpAKFFwS0OqmWh9dI0o3MEnmeHDQzsVIOQ7YpACYSSt0/JfbZYH032/zmg6dMQfwc8ESxR5liyKOxsip3q4VigJwRMp2yzmlDrs6aNVBU5dKmpGDh8pMel6EUs58VP6vgGYFM/VLNsjMSOTDnqxN+WfFy0mJ6MKT2lgDcBagEpYSAB3vd35r/NfzP/YT7T1uJj14vsWi29FkTz56V67G67RSHlrHLknTlOAwu1OFWPNVSu03VcCdm0+tGtUzTya9kr691IQ4VuXPIcapPWqRyupUem1IwU0Daagy38IZB4WBwMwvcXwzSWeI+UACPv3MoKBn87+YuErwl4rduI011o75zdEauOmwkae2xa554MvW8twpI6FqswIoac/2P8u9f/N3kDNx8qFLLg8M61Jc+UWG6ea/N8HCZ/XbQ7oeePAQNC/hvJVqaNQQEfgBfQXwxy/CryfM4Sz97r01gjIT22rRkBSf0Z9/m2n5yx+4/rsHWYpNjxhb93/t8lC94m5N4QgeLyOoo9xvvGWrNnWUtTF0KXM2Drf4z/xzlkdVsg1V6z68xVdTal1+kcneu7Zdw9kp+t17IWcXjPfBHIkNE7H3VQEuNLB0B/VvpKUsDCJ0Xd4PlM6NnAsnf4VQCuIQfhoUujVUQHShLtraWs/xtx6adyPwW8KkTEygcCAKKANDTRZbWkHXFNNd97fSwnQUh8GGhLhhnROxvfm5fP38BcviyRm7KucMqqN8a6u+jeveljQIE3cTccOjo6qgE6UL8c3wIAvuS7NFjo8jguKyfnFzQanZuV5Rq58YXdLS5dapr+or//ikOdr30V806aEzWkd1ivOElNMkn06DTKmuxY76YXuVEDYKFu5Mbz6LVOHe3A380dmmMaiddq2zW1tPx6S0zqguZQYPaxNgDiuJJSUu62ZAxO1143hD3dgm29K6837ObuzmUmHYB+DuH1lppxJ8iYxuHpmZmC0w/zAHYF7AZndvaikJp1R0+t+O2upTEq602iyMbWXNEIwI1Yo/VBWITl/aJYHqOktJS1u7VGurA83ui3+5WtHb76e8rEhKRKG/CVuHgosUD2pbviW6Br+U6+usUL3L55Ir4rmdMYcx+gQMM1Xn2+Q5Wu2PFUKSXfV3H7SDR9/ryn4Y+0/UpqI11aM6Ahn/uV04A2U1Z2gkIOCgoa8y95pFDt0RnYBzCl2rNBs3aBgS86ixAT2v7jv8IwYODOrwiA/zBDeECQY179QNjfmhj06fbm8rI6odAw1Po0aweDuB8hjNtMXJzXCnjwkGANghQAjb6e/+pNfLRzWASA2ZBpk8yZ1rtC6dNNKvDg9sc/fNDE9Sf0oC8VJ1iXV3l0yoD3Hx7ztqHIZdhVuQkQx/gJl4rq8vPlQuOUvcppWBrMPGV+o0jt4YAdTtLpKp6zMHjCwFiE708++039ywWEbyWJjTjuzss8qoYJArg3yMIEZUwydIn/B1BLBwj7JnAkawoAAKILAABQSwMEFAAIAAgAGII8QgAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAAIABiCPEIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V35ctvGGf/beYotM+NJpxKEXVykLcXjuE2bjuJ4ZLfpMZ0MCCxBhCRAYUEdmTxA+xT9q9M+V56k3+4CEHjgIgFZMpTWAhbY6/vt7zv2IHn66mYxR1c0Yn4YnA2wog4QDZzQ9QPvbLCKJ8fDwasvPzv1aOjRcWSjSRgt7PhsoCtkcFcOUgrWeGHfPRtMbHeoa6Ph8dAko2OdTNxjezSxj3XVmUywZWnGZDRA6Ib5L4Lwrb2gbGk79L0zpQv7PHTsWNQ5jePli5OT6+trJW1dCSPvxPPGyg1zBwh6HrCzQXLzAqpbK3StiexEVfHJX749l9Uf+wGL7cChA8SlWvlffvbs9NoP3PAaXftuPD0bmCZ0bkp9bwpimiNtgE54piXIuqRO7F9RBkVzSSFzvFgORDY74O+fyTs0z8QZINe/8l0anQ1UhYyGI0MzTYKHRDOxZQxQGPk0iJPMOGn0JK3u9Mqn17Jefiea1NWRBWPgM388pxz1OQOx/GASAaTQo2gFSRbfzunYjtL0XYfwEfwPMvg/UV4XjJ3E4WxAVPMIG8aRpapHhqHKvuQbHqA4DOeiVhUZI/Tzz4ioREVH/ILlhcDFNOUrVT5TNXkh8qLLiyHz6LK4LrPqMo8u8+haiZxJ+k7Q5MGapKmcWl5ODPLxfyb8EwBsyDnMyYm5ED8jzHsvLhri/cai//yiJ0lTJi1xwaq84OTlkP8ReJkHSqTtJRHOtSr5UNzoFl/SFk1jWL9FcpCcmZRkl5TEKJDyQHDTRrGRaxTaEv8X/7aa1BrJWQhtgxZN/RDd36NBS11T+1Tn5RUn1zIYWuvU6UlqDU+TDiE25XkTSsd0wXgXtZEwTggjA5TXtMCWGAiP4GJxJSYIG0g3IImHyORXC2lcb3WkoSHi+bCGhAkyhvBHFzptIgPq4g8tqdxI05GhISwMl44ABSSMH2BCNMhhGMiAQrx1zJvVTKSbkNCGSIcOcrNncdOiQTlIQ+MEaRhpvCy2EDGRSZDFTSfWuUU1h7zvUClBpopMXhRsJ9hNaTOhxBBpXBrQgmXI/AzcKZ0vs1EROPrBchWvYecs3PQ2Djdyu6Ez+2oDa2qzOL2HTOCw7vyidGBrbvPZ6dwe0zkEF+85DRC6sudcy0X9kzCIUUqBoXzmRfZy6jvsPY1jKMXQj/aVfW7H9OZryM3SDoqmhTc/pStn7ru+HfwZOMKr4BWizLlz25U6d8MwZStOGEbu+1sGxEE3f6NRCO8sRc39h4HYt/KNbhJllP8PFJE5Nme8oa4VUuHNbcErrMum6VUmmn1DM4GQF8lIKkt8w74K53ePlqEfxG/sZbyKRKgGljLiUr0OvDkV4Ioxh6DHmY3Dm/cSVU3W9eF2CSlV9mDsvQnnYYRAI4kBgYiXXMfyKvLwrmW5VJFHFTnUdJh8N3uPR0TkENexvIpcMO6ya4moOBUTq2kzPhO2BiqXLEuNM2cNj6FWgR+fp4nYd2Z3ovICb1eLMRAuYeR6nbitOk9PNjh2OqNRQOeSSQEM5ipcMUntjJ7PTleMvrPj6evAvaAe6OQ7m5vFGKqWWe+67FLHX0BB+TwBz+YD+yfoqnzqUi+iqYhzER1LaMVbNc/rrceiqq+jcPFNcPUBWLPR1dOTVJ5T5kT+krMTjcFOz+gd/1yf2WDl3Xw5EJ6BFA63OABkzEH8Nowgt72Kp2EkgmDQXZBpiP5oBys7ugVzCawUUXgYzdiU0vgDvYmRPQ6vIOOHKUUewPQCrPVybt9ytIBlMbUXTHn+OVZffgdRNk8ij8YMxVOeCpBwOcgOXPEkhD/RRi7Xd6iC3kWUyfRbcHPJUIPp4/mQzYFZQa7vwQRNZfmpzdACZEJuGLNX6MPUjuUL5sBTUGKpmQr62o9Y8gqqs+Rjxt1a0nHx5/0KDCRoqT2f08ADMcVTLHPzyZbo22Strojac27Trqdh1h0FfaEif8Jz3yJvxYWShcZg4G3o7nUUBp7ya/TBh05y4dSkR8rOFmVbXLisBZHvHYwB7wN4sqQ4qDidc7UCMlEW+57w5i9E7m84tD4HZWL7kRjIVwA5jCy6DVeipRAocO3HU04MOwcM5w36PQ1/L2ad0A+YdU6n4WIMPQEuemwZxooTLhLiLRZ8rAMRZ7wL57deGAzuPJytng2+UI+Q+mugIpb3mN8TuMfJvSbvIY9QknAVp0WXUCGWJW1ZaCzzO3DRQRel1iS94D5oThcwmUOxsLPLpD+pxZHVrRtEgMmZwVSPydlVYp/FzR9816XCg4t+cZOEwvGP4FOzEErWm7M18H7DXGNVGmODCzJfTm0+DVUT8y4Ua81EiCq/Dd284QC7J+XakpBRj6eyntiD1nvapKOJ4WPo5mxwLJY0bmUd6Kd8XXuAD6SY34I5/CbgdpsKS7dt6WeULrmL/S74ENkB40sm6ya+PpLjh4OkmgCJEyAFso8HSefhILlJyUeGpPtwkEw5eYwfqHave6YLuAWXte6YEs9ibrmdCy2g1+WuJVgtaOQ7GfSyiFgv5JGL7JeRYrI9GmkQfzcUuFUJSHMJyA4J8MeTADeXAH9ECYi6JcJ5YwnOdwlgHiTBeoNXoFthlLW32jYo63O0Uouy3XpDc2IHMNsScxYW06Wc9y0plVPGzF7w2YeYaec6U2zSy+0QKbdDuWkbk1NRx45iymDC2QjX4PHjuhl03Beu6xonDP0cZq4bSpebGAS7Zw3P7WXIXu4xP0gKPu5ZQgMUE3mrsTwQ0X7i2hDdVjDuM9LVeJPm6JL+YCmRW5Ux9Qe8Nz9/eOyrL3va1VI8D0a1r9g2RLglnPuNdjXmWnN8td5gScqQI/t6f9JPj/9DqbfSm+Oot4Ngg6neR4NQL4VuXyLqPSOiXm0O9cMCe72XIb1eHcbrhzr1zQp6hu26Cd2NsdEcVaM3OBqlyO2r70bPNN2o1nTjMAtq9NmCNrSjrXipPiNdjbfZHF2zN1iapcjty06zZ4w0a7DwMH03P1lNLzjCNswdYYN7kh1hU5OEliQKDrFZsiyVxSaygCcPsU2b428VY250gvmBW5L1j7jQQ464HLxxmju9Rjb2le+24feB/d6PCk0eCI7pNjJJT1zpjwpG74HAuMnGY1K+H//QcJw+EByzY2uk1rGGjw3j5rGST+hcCVGMB3quJPHVwe7Iydo3ZrKqoqUH77nXIXzjR858E78vVMWAIEgxkmBJVXRjC8ZZOXhOGOSOxM3qWw4o6PqSnpD9uyT3OfrlX/9BeBuf9DNX2wjppJle7ENd6ns0kPrNELpR05Nsamrk0yc3AOOx1BqcHsfCuXONoJGRf4Nep/lfp7lekzPxgXf+GffXWlLta13Uxh8ZyZ3szmWwpkf8o4P+BMZhLzWaFc09ZnW0Z4MAOb05mAaknzQgFTTAHdGgfCI6qz8J3UmJNomh9ZMYJieGnvtIbTFHSKccacCUA/nSJmv0frIGV9kT7R64UrHI1YQfy3bYYPSTDaQqyNC7YcOycNu9uYVYtmkV0g/V944Iu80C7poIhWZhmxqXTUhx2Q4dRv1kA9Yr2HAfTqKIBzsoU3WGpDKkSM6QHMyXYT/5MqygS7fxZy2iHECRtshh9ZMcetU8BXc+l61gyF7caIsVZj9ZURVvdLW6VXX8OGpChWjPNf0+DHDl8gTpeqyjwjFuPsmIWp1k7FjRzq/4C3p8gpQoWHvQuiZCfgunxv7QgbtEn9heUaF2lQdf0b4LftEWiofr2w4f2wd9K1jd0Ts3vOXre9H+cflm0XbosWNnqQ/0KJjla12H45uDWEAT1oQYrCUq7NhL6gUVds/gta5n8Kxw8Js7Dtaqy9ixPdQHIpAqm9DRyh8rdxls32iCdRBN7Ngr6gM1tKrovaMtgvWAsE5McWDQ2SpZdiz69YEsBftJ+r3GFuWUiZsQJG6JDjs2CHpBB7OCDh3FF3Hh4De3EXGrdmHHzmIfiFDgRPSu44u4whbs6zji9l1G9m2UPaOGXrVacWB8sfvQ81DR+KFnLTv0TLYPPTvNFimcwxcmLjBQ4d+IoF/++T+UJPR8wswnKgLSu0XBbCAeP1vMoTLClpH9NAjZ5A0MbLbKpXXEG6xYZbxxm/HGbY032hNvinhjwZjV5A3k7Io3ZayhzVhDW2NNxSr5J0kHc6QMSY4OuIwOavt0GFWQYdKMDJPWyIDzhkLru9UYYmWkbccmI3HXHTkUqzI28ZoRxHvyMd2zZaQrGOfPPmzzxuoyNhG8KTUr02asmT75mEPoYCgqqUeH7sxIRag6a3gG7mmKcw+8MfkUpyZvDgpVi1ZNnGx3dseBmWaMWbbAGJJnDMkzhuQZQ3rLGMtUTLPe5IYowy4YQ0sYc9mMMZetMaaPTgciVtWqN7HpaMnVLaFC1PDYT2tU0J6MRyFjTEWvaTx0hXTBmEkJY1gzxrDWGIPzvND6TpKRpuBh2US4I2PilVAjbkaN+MmY3MOBMhUrQ7Ne8NpRKDItoYzzQ8VPyWzu6JCnUOQALpgKsepxoasPlpZwwW3GBbc1LjxNZIopgzGfydSiTEfByLKEMrQZZWgLlNHylNHylNHylNF6Sxm5WlIrfDUOW3QtYsxlCWMmzRgzaY0x/XQ4eu1dveyrYetyYX3Ytn4FdvMnYLPPYZV8SjT9Msl6n+vCNYcpybfvFz/ucfayhP9eM/57rfFfe7KYxU5Wq30Wwmy6wFyuJhe4x3rCSvRk2kxPpq3pCc5rg/akGmbFhn/LfuOCfJIKUSG09kkKXfNEcokVmDWzArMnb3kfX15Aap/q6GiCwZehirdjG1Fm+TTBOIQLmrp+pMMq5kJjR1F3d62YC5fNuHD5tDxxH5SRB9bLiHJQiD1exXHuC0lksmqno5kvLR+M7yYTRmPxixeWLn4nQNfKxmr/XySwVzf+3Lej2/XfYnh26nlj5kT+MkbyzZ+WLmjOmzBgkEf8xMPf//H8c6y+fE/jP/Oo4+/nR+cBvd54eIGPLvCOx+Togux4rB1daNljjvVZXl/spZBR9OctvUZvV4sxjdjWYN4sI2Arz5pGRwMED8VBqd/wtWD4A7Oxk+qoqjCoqh0vlXcspjcxTjr3/HIVxi+/n4ZoajO0CCP6Sj4abHeUlxusV1Lb7LT+hTfPTich9IwBdJMswmT+T/RbrrS6vD8bDAepFqYB4piF81VM3zsRpcF56EgKC9rrpqC9ZuyhqVUmuBtNxcSQmjokH1lVM3UCsq3m8VFMg0kEHjCnVXeF15TqAw3Q1zzrHqhrHwV1jrZA3Ro+MNRd36mB+G8h1x5g6x8FbA1jAfbwoWFNL1f2fANskdqB+O943nqWmaxZ5r9S9qv6BvngOFCKJoI8XhCCvv+K99mT7fHFxCr8cOu9WHQW21H8LvShLOeLoahG7lsLRzKUgSjeyj+15A/LyR5WD4q2NihvptSZITHWtmf7QYMRqjJYTUZI5K0zRGry240fyeVuDJCuDLX8UBjJAOG1ATILB2jdUIXhnNp3lkrCsxlB3cHS2rpUI+Tq95/3b7P3OU48gO5v6Qf3OWmoi5578Ut0vivM3ZRUFHtckqYxTSLtuZT2oo60WdHHJbHwcZm43MLUklYWe8BKeOLk5pQ87dHQo+PI/vL/UEsHCNMmmJpxEAAAHKwAAFBLAQIUABQACAAIABiCPEL7JnAkawoAAKILAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAIAAgAGII8QkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAArwoAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAYgjxC0yaYmnEQAAAcrAAADAAAAAAAAAAAAAAAAAANCwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAALgbAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="false" showMenuBar="false" showToolBar="false" showToolBarHelp="true" /> | ||
| Line 11: | Line 41: | ||
<br /> | <br /> | ||
'''2) Objectives''' | '''2) Learning Objectives''' | ||
<br /> | <br /> | ||
| Line 19: | Line 49: | ||
* representation: to subitize | * representation: to subitize | ||
* representation: to compose/decompose small numbers (<=20) | * representation: to compose/decompose small numbers (<=20) | ||
* addition, adding small numbers and encourage strategies that use | * addition, adding small numbers and encourage strategies that use 10 | ||
* probability, comparing two different random sets of data with different ranges to determine fairness | * probability, comparing two different random sets of data with different ranges to determine fairness | ||
Latest revision as of 16:35, 1 April 2013
Lesson idea. Geogebra has been used to create a simple interactive applet. The applet and guidance notes on how to use it with students are included with the resource.
| Resource details | |
| Title | Number and representation game. |
| Topic | |
| Teaching approach | |
| Learning Objectives | |
| Format / structure | Embedded GeoGebra applet and guidance notes. |
| Subject | |
| Age of students / grade | |
| Table of contents | |
| Additional Resources/material needed | |
| Useful information | |
| Related ORBIT Wiki Resources | This activity is a result of the 2013 ORBIT/GeoGebra Competition that asked entrants to create an open-ended activity that supports interactive teaching and active learning for the 6-10 age range. |
| Other (e.g. time frame) | |
| Files and resources to view and download | |
| Acknowledgement | John Golden |
| License | |
Guidance notes
1) Overview
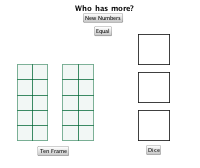
This game is a variation of War that emphasizes representation for number. The ten frames are filled with a random number from 1 to 20, and the three dice work like regular dice, each having a random number from 1 to 6.
2) Learning Objectives
Use the applet for the following:
- number sense, to compare two different values
- representation: to subitize
- representation: to compose/decompose small numbers (<=20)
- addition, adding small numbers and encourage strategies that use 10
- probability, comparing two different random sets of data with different ranges to determine fairness
3) Teaching Approach
The sketch is usable in several ways: as a visual to discuss number representation, addition strategies and comparison; as a game that encourages number sense; as an investigation into probability and whether it is a fair game.
4) Teacher's Note
I would use this with the whole group briefly, to demonstrate the various buttons. Then encourage students to play in teams of two. First the basic game, who has more, then with the challenge of determining who has more. If that is too competitive, teams could take turns being the judge of who has more.