Variety of areas with fixed perimeter

Interactive GeoGebra investigation that allows children (age 6-10) to explore an element of mathematics for themselves.

Lesson idea. Geogebra has been used to create a simple interactive applet. The applet and guidance notes on how to use it with students are included with the resource.

Resource details
Title	Variety of areas with fixed perimeter.
Topic
Teaching approach
Learning Objectives
Format / structure	Embedded GeoGebra applet and guidance notes.
Subject
Age of students / grade
Table of contents
Additional Resources/material needed
Useful information
Related ORBIT Wiki Resources	This activity was a result of the ORBIT/GeoGebra Competition that asked entrants to create an open-ended activity that supports interactive teaching and active learning.
Other (e.g. time frame)
Files and resources to view and download	GeoGebra file: File:Variety of areas with fixed perimeter.ggb Guidance notes: File:Variety of areas with fixed perimeter.doc
Acknowledgement	Anthony Or
License

Guidance notes

1) Overview
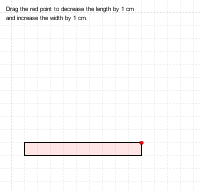
After learning the concepts of perimeters and areas, it is easy for students to think that figures with larger perimeters would also have larger areas, and vice versa. This applet helps teachers to explore with students the variety of the areas of a rectangle with a fixed perimeter. Together with the complementary applet Variety of perimeters with fixed area, teachers can clarify with students that a figure with a larger perimeter may have a smaller area, and areas and perimeters are two different concepts.

2) Learning Objectives

• Recognise that rectangles with same perimeters could have different areas.
• Recognise that among all the rectangles with the same perimeters, the square has the largest area.

3) Teaching Approach

An enquiry teaching approach is expected. Students are asked to shorten the longer side and lengthen the shorter side by 1 cm each time and visualize the change of the area, and investigate when the area would become largest. Teacher then help students to express arguments which justify their conclusions.

4) Teacher’s Note

Ask students to record the dimensions, perimeters and areas in the table of the applet. Remind students that when the longer side and the shorter side are shortened and lengthened by the same amount, the perimeter is unchanged. Guide students to visualize that the area would always be increased if the longer and shorter sides are changed by the same amount until they become equal. Another way of arguing is to begin with a square and then change the longer and shorter sides by the same amount to see that the area must be decreased.