Square It: Difference between revisions
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
|Learning Objectives=Thinking strategically in geometry | |Learning Objectives=Thinking strategically in geometry | ||
|additional resources= | |additional resources= | ||
|useful information= {{nrich|http://nrich.maths.org/2526 | |useful information= {{nrich|http://nrich.maths.org/2526%20Nrich%20Square%20It}} | ||
|related resources= | |related resources= | ||
|other= | |other= | ||
Revision as of 15:45, 21 September 2012
This resource may not be final.
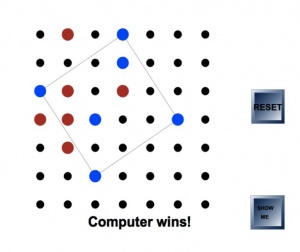
Lesson idea. Players take it in turns to click on a dot on the grid - first player's dots will be red and the second player's (or computer's) will be blue. The winner is the first to have four dots that can be joined by straight lines to form a square.
Teaching approach. This lesson idea is about thinking strategically(ta).
The collection of NRICH activities are designed to develop students capacity to work as a mathematician. Exploring, questioning, working systematically, visualising, conjecturing, explaining, generalising, justifying, proving are all at the heart of mathematical thinking.
This particular resource has been adapted from an original NRICH resource. NRICH promotes the learning of mathematics through problem solving. NRICH provides engaging problems, linked to the curriculum, with support for teachers in the classroom. Working on these problems will introduce students to key mathematical process skills. They offer students an opportunity to learn by exploring, noticing structure and discussing their insights, which in turn can lead to conjecturing, explaining, generalising, convincing and proof.
The Teachers’ Notes provided focus on the pedagogical implications of teaching a curriculum that aims to provoke mathematical thinking. They assume that teachers will aim to do for students only what they cannot yet do for themselves. As a teacher, consider how this particular lesson idea can provoke mathematical thinking. How can you support students' exploration? How can you support conjecturing, explaining, generalising, convincing and proof?. (edit)
| Resource details | |
| Title | Square it |
| Topic | |
| Teaching approach | |
| Learning Objectives | Thinking strategically in geometry |
| Format / structure | |
| Subject | |
| Age of students / grade | |
| Table of contents | |
| Additional Resources/material needed | |
| Useful information | The resource has been derived from NRICH, and is available here [1]. |
| Related ORBIT Wiki Resources | |
| Other (e.g. time frame) | |
| Files and resources to view and download | |
| Acknowledgement | |
| License | |