Changing Questions Description
| Pedagogical rationale | Test questions are often seen as uninteresting and a way to assess pupils’ summative knowledge. The approach here uses such questions to support pupils’ revision, creativity and problem solving in the classroom. |
Learning Objectives:
- to be able to use an existing resource to deepen understanding in an interesting and creative way (for a lesson starter or all of a lesson).
Introduction:
Many test questions, particularly at GCSE, are uninteresting and test a single piece of knowledge. However, the questions for the KS3 national tests in England (often referred to as ‘SATS’) were often interesting and much more challenging. Consider the mathematical knowledge that is required to be able to answer the question (from 2007) below:
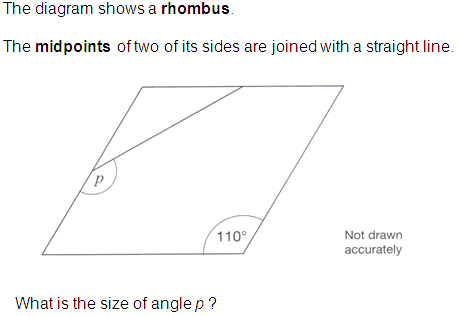One way of answering the question requires pupils to know:
- the properties of the sides of a rhombus
- the meaning of the word ‘midpoint’
- the angle properties of a rhombus (or to use parallel lines)
- the properties of an isosceles triangle
- angles in a triangle
- angles on a straight line
This is a great question to use with pupils in a lesson because it is not trivial. It may be worth asking pupils to reflect on the different forms of knowledge that they need to be able to answer it.
Changing the question
There is more to be gained from this question, though, by making sensible, structured changes to it. For example, what if the angle that is marked as being 110° were to be changed to become 120° ?
First of all, the pupils can consider whether angle p will get bigger or smaller and whether it will change by 10° or by a different amount. Then they can work through the problem again to discover what happens. This is useful because it allows them to carry out the calculations for themselves even if they were not able to do it the first time the question was asked.
It is fine for the teacher to suggest changes, but more exciting for the pupils to consider their own changes. They can now be asked to make suggestions of their own. For example, what if the angle given shrinks by 10°? What special cases are there? [Can the given angle be 90°, can it be 0°, or 180°?]
Finally, the pupils could be encouraged to use algebra, perhaps with x as the starting angle. This demonstrates the power of the algebra, because if they had done this first, the other calculations they had carried out would be largely redundant. It is useful for the pupils to be able to suggest their own changes because they will be more heavily involved, but also because they may well have different, exciting ideas that their teachers haven’t considered.
The resources
There are over 80 questions from the 2007 papers that have been presented in a form (on PPT) that is useful for projection in the classroom. The first slide is a teacher crib-sheet to glance at before the lesson starts. It gives information about the question level, the topics covered and suggests changes that can be made. The following slide/s hold the question to project for the pupils. It is likely that the teachers’ notes pages will need to be updated to reflect the new ideas that pupils come up with during the lessons.
