Circumference of a Circle
Lesson idea. Geogebra has been used to create a simple interactive applet. The applet and guidance notes on how to use it with students are included with the resource.
| Resource details | |
| Title | Circumference of a Circle. |
| Topic | |
| Teaching approach | |
| Learning Objectives | |
| Format / structure | Embedded GeoGebra applet and guidance notes. |
| Subject | |
| Age of students / grade | |
| Table of contents | |
| Additional Resources/material needed | |
| Useful information | |
| Related ORBIT Wiki Resources | |
| Other (e.g. time frame) | |
| Files and resources to view and download | |
| Acknowledgement | Irina Boyadzhiev |
| License | |
Guidance Notes
I. Overview
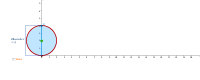
This applet can be used for introducing circumference of a circle. The students can create circles with different diameters by dragging the blue point D vertically. The circle can be rolled along the x-axis by dragging the green point - the center of the circle. This will “peel off” the red outer layer and transfer it to the x-axis. When the circle is rolled to the end and the entire red line is transferred to the x axis, a slider appears. Dragging the slider the students will see that the diameter fits a little more than three times in the circumference. They can record the diameter and the corresponding circumference in the spreadsheet and calculate the ratio circumference/diameter.
ll. Suggested activities and learning outcomes
1) Learning some basics about the circle and disk.
- Drag the blue point D up and down to create circles with different diameters.
- Click the Radius checkbox. See the relationship between the radius and the diameter.
2) Define circumference.
- Drag point D to select a diameter.
- Drag the circle by the green point to transfer the red line onto the x-axis. (If the students have seen the Perimeter of a rectangle applet, they can be directed to discuss the similarities between the two).
3) Find the relationship between the diameter and the circumference.
- Drag point D to select a diameter.
- Drag the circle by the green point as far as it can go.
- Drag the slider to fit the diameter into the circumference.
- How many times the diameter fits?
- What is a rough approximation for the circumference of the circle?
- Record in the spreadsheet below the diameter and the corresponding circumference for several circles from the activity above.
- Calculate the ratio circumference/diameter.
- Introduce Pi.
- Write a formula for the circumference using the diameter.
4) Experimental approximation of Pi.
By finding the relationship between the diameter and the circumference, students discover that the circumference is proportional to the diameter (C=kd). Drag point D to make the diameter equal to 1 in order to approximate the value of k.
III. Learning Objectives
- To introduce the circle and some basic terminology by actively manipulating the object.
- To introduce the circumference of the circle through a dynamic process, connecting the new concept to a familiar one (the perimeter of a rectangle).
- To introduce the constant Pi and approximate its value.
lV. Underlying pedagogical/teaching approach or rationale
The applet gives the opportunity to involve the students in the process of teaching. Each student can create and manipulate the circle, learn terminology by manipulating the objects. Students discover a relationship based on experimental data and mathematical calculation. The explorations can be done fast and accurate.